编译原理期末复习笔记-正则表达式->DFA分析题

期末复习
3.1k 词
阅读次

目录

  1. 1. NFA转DFA
  2. 2. DFA最小化
  3. 3. 最小化DFA转词法分析程序

要求：会写正则表达式、画NFA、画DFA

熟悉实验二的流程：词法分析程序getToken()、正则表达式转NFA、NFA转DFA、DFA最小化、DFA生成词法分析程序

简单一点的：手工方法画图

难的会写代码，以及各个流程的具体代码（需要明确具体的各个流程之间的转换代码）：

  • 定义数据结构

  • getToken解析源代码

  • 高级正则转基本正则：如a+->aa*、a?->(a|#)

  • 再对基本正则转NFA

  • NFA转DFA

  • DFA最小化

  • 根据最小化DFA写出词法分析代码

NFA转DFA

  1. 求Epsilon闭包：求A状态的Epsilon，就是求从A出发，可以通过Epsilon转换到达的所有状态

  2. 消除多重转换：子集构造法

  3. 例子

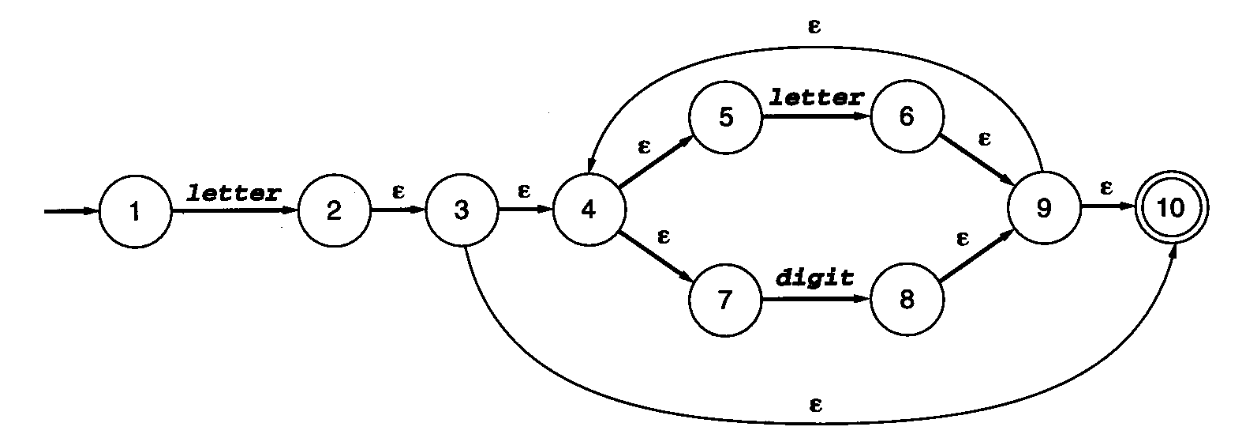
image-20250628171314699

  • 先求始态1的Epsilon闭包：{1}（1没有到其他状态的epsilon转移）

  • 然后看图，发现除了epsilon转移，还有letter与digit转移，画出表格框架：

    状态集合 letter digit
    {1}

  • 接下来，进行子集构造：分别寻找{1}通过letter与digit转移可以到达的状态集合（包括借助epsilon转移可以到达的状态，在一轮寻找中，letter与digit只能借助一次）：

    1. 寻找通过letter转移可以到达的状态集合：{2, 3, 4, 5, 7, 10} （为什么没有6？因为只能借助一次letter），然后将找到的状态集合填表

      状态集合 letter digit
      {1} {2, 3, 4, 5, 7, 10}
      {2, 3, 4, 5, 7, 10}

    2. 寻找通过digit转移可以到达的状态：无，不填

  • 我们接着对新状态集合{2, 3, 4, 5, 7, 10}进行相似的搜寻，分别找到通过letter转移可以到达的状态集合{6, 9, 10, 4, 5, 7}，以及通过digit转移可以到达的状态集合{8, 9, 10, 4, 5, 7}，之后更新表格

    状态集合 letter digit
    {1} {2, 3, 4, 5, 7, 10}
    {2, 3, 4, 5, 7, 10} {6, 9, 10, 4, 5, 7} {8, 9, 10, 4, 5, 7}
    {6, 9, 10, 4, 5, 7}

  • 接下来再对{6, 9, 10, 4, 5, 7}与{8, 9, 10, 4, 5, 7}分别求解，得出结果并更新表格……一直求解，直到不再产生新的状态或转移。最终表格如下：

    状态集合\符号 letter digit
    {1} {2, 3, 4, 5, 7, 10}
    {2, 3, 4, 5, 7, 10} {6, 9, 10, 4, 5, 7} {8, 9, 10, 4, 5, 7}
    {6, 9, 10, 4, 5, 7} {6, 9, 10, 4, 5, 7} {8, 9, 10, 4, 5, 7}
    {8, 9, 10, 4, 5, 7} {6, 9, 10, 4, 5, 7} {8, 9, 10, 4, 5, 7}

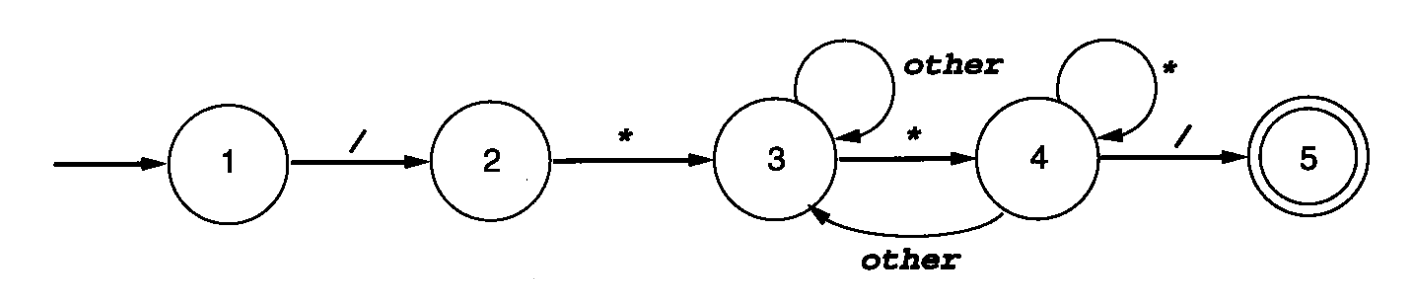
  • 完成后，即可根据表格画出DFA图（记得给NFA接受状态10所在的的状态集合画上双圈，表示DFA的接受状态）：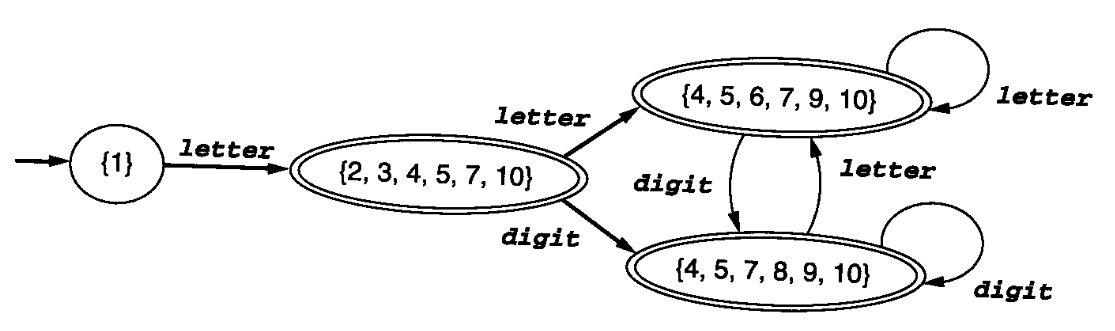

    image-20250628172949919

DFA最小化

  1. 将原始DFA分为接受状态集合S1与非接受状态集合S2两个集合
  2. 对S1与S2里面每个状态，分别判断它们通过所有的符号转移后，得到的状态集合是否一致？如果一致，说明它们同属一个集合（可以最小化为一个状态）；如果不一致，则划分出去成为新的集合
  3. 例子1：

对上面的DFA，令

A = {1}，B = {2, 3, 4, 5, 7, 10}，C = {6, 9, 10, 4, 5, 7}，D = {8, 9, 10, 4, 5, 7};

状态集合\符号 letter digit
A = {1} B = {2, 3, 4, 5, 7, 10}
B ={2, 3, 4, 5, 7, 10} C = {6, 9, 10, 4, 5, 7} D = {8, 9, 10, 4, 5, 7}
C = {6, 9, 10, 4, 5, 7} C = {6, 9, 10, 4, 5, 7} D = {8, 9, 10, 4, 5, 7}
D = {8, 9, 10, 4, 5, 7} C = {6, 9, 10, 4, 5, 7} D = {8, 9, 10, 4, 5, 7}

现在根据是否为接受状态来划分出两个集合：S1 = {A}、S2 = {B, C, D};

我们观察上面的表格，发现对于S1内部的状态A，通过letter转移到S2的B；而对于S2内部的三个状态，它们都是通过letter转移到S2的C和通过digit转移到S2的D，说明它们三个确实属于S2集合，S2集合无需再进一步划分，可以融合为一个状态。

最终，我们根据S1与S2得到最小化DFA：

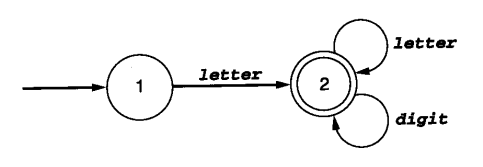
image-20250628194253250

  1. 例子2：

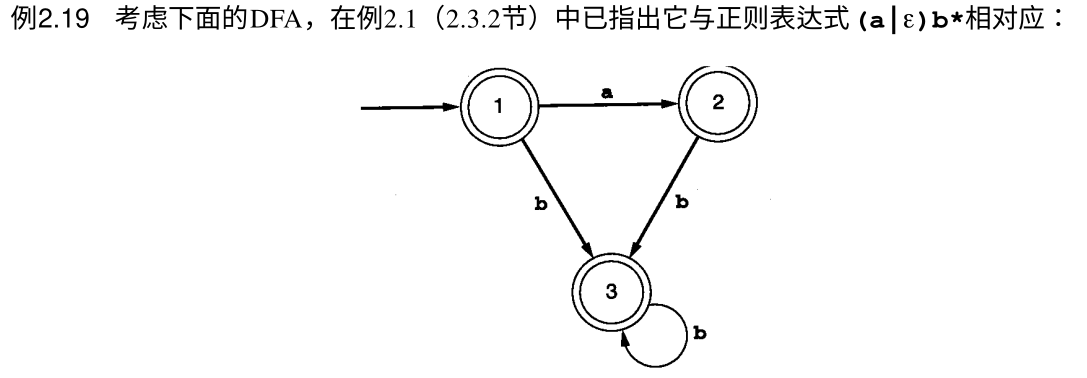
image-20250628194353377

来看这个DFA，它们都是接受状态，因此我们先划分一个集合S1 = {1, 2, 3}

然后依次看里面的三个状态：

  • 状态1可以通过a到达状态2、通过b到达状态3
  • 状态2可以通过b到达状态3
  • 状态3也可以通过b到达状态3

我们发现，状态1和状态2、状态3不一样，因此S1分裂为{1}与{2, 3}两个集合

最终得到最小化DFA：

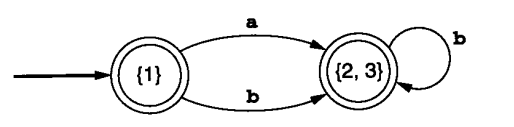
image-20250628194907816

最小化DFA转词法分析程序

image-20250628194253250

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
int state = 1;
char ch = nextChar();

while (true) {
    switch (state) {
    case 1:
        if (isLetter(ch)) {
            ch = nextChar(); // 接收下一字符
            state = 2; // 进入下一状态
        } else {
            error();   // 出错
            return;
        }
        break;
    case 2:
    	if (isLetter(ch) || isDigit(ch)) {
            ch = nextChar(); // 接收下一字符
        } else {
            accept();  // 接受状态
            return;
        }
        break;
    default:
        error();
        return;
    }
}

image-20250628200951413

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
int state = 1;
char ch;

while (true) {
    switch (state) {
        case 1:
            if (ch == '/') {
                ch = nextChar();
                state = 2;
            } else {
                error();
            }
            break;
        case 2:
            if (ch == '*') {
                ch = nextChar();
                state = 3;
            } else {
                error();
            }
            break;
        case 3:
            if (ch == '*') {
                ch = nextChar();
                state = 4;
            } else { // other
                ch = nextChar(); // 接收其他字符，停留在状态3
            }
            break;
        case 4:
            if (ch == '/') {
                ch = nextChar();
                state = 5;
            } else if (ch == '*') {
                ch = nextChar(); // 接收*，停留在状态4
            } else { // other
                ch = nextChar();
                state = 3; // 接收其他字符，回到状态3
            }
            break;
        case 5:
            accept(); // 结束
            return;
        default:
            error();
            return;
    }
}
留言